Mapping class groups
Spring semester 2024 in Fribourg
Lecture: Tuesday 10h-12h and Thursday 13h-14h.
Exercises: Thursday 14h-15h.
Location: room 2.52 in PER08.
Content
The aim of this course is to give an introduction to surface mapping class groups, mingling algebraic, topological and geometric aspects of the theory.
Particular topics of the lecture include: curves on surfaces and intersection numbers, Dehn twists, generating the mapping class group, the Lickorish-Wallace theorem (stating that a compact 3-manifold can be obtained by surgery on a link in the three-dimensional sphere), the Dehn-Nielsen-Baer theorem (relating the mapping class group with the outer automorphisms of the fundamental group), pseudo-Anosov theory.
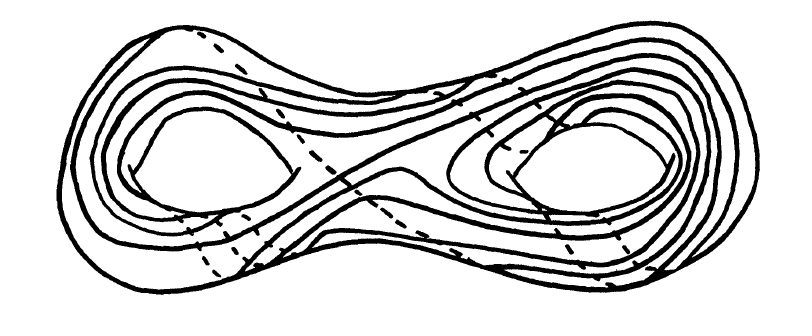
The image on the right depicts a closed curve without self-intersections on the closed orientable surface of genus two. It is taken from Thurston's research announcement from 1988 about his pioneering work on surface diffeomorphisms.
Prerequisites
The first two bachelor years. Knowledge in Riemannian geometry, geometric group theory and algebraic topology is nice to have, but not required.
Program
For our weekly topics and the exercise series, see the course's Moodle page.
Literature
The primer is our main source for this course:
B. Farb, D. Margalit: A primer on mapping class groups
Further reading:
B. Martelli: An introduction to geometric topology
S. Katok: Fuchsian groups
A. Fathi, F. Laudenbach, V. Poénaru: Thurston's work on surfaces
