Complex Algebraic Curves
Fall semester 2022 in Fribourg
Lecture: Tuesday 15h-17h and Wednesday 8h-9h.
Exercises: Wednesday 9h-10h.
Location: room 2.73 in PER08 on Tuesdays and room 1.309 in PER07 on Wednesdays.
Content
A complex algebraic curve in C^2 is the zero set of a polynomial f in C[x,y],
for example f(x,y) = x^3+x^2-y^2+1. For a long time, the study of complex algebraic curves has been intertwined with ideas from algebra, number theory, topology and geometry, and became a central topic in modern mathematics. This lecture follows the book Complex Algebraic Curves by Frances Kirwan.
We study complex algebraic curves from an algebraic, a topological and a complex-analytical point of view.
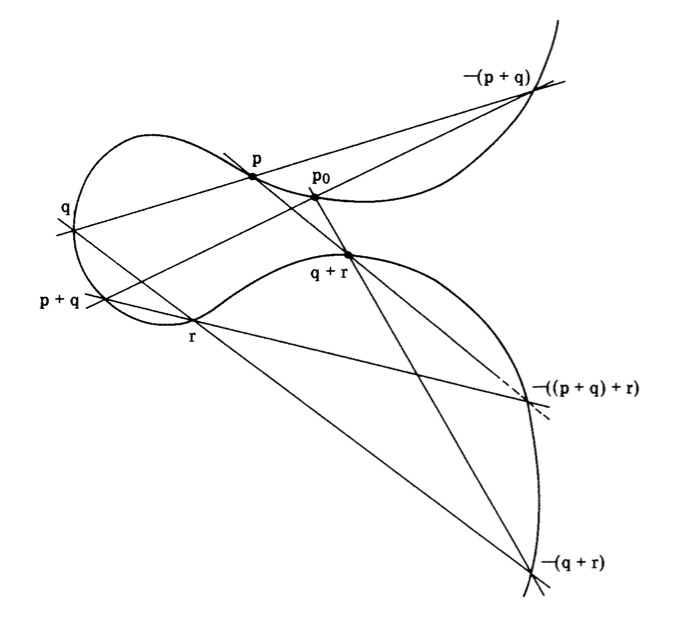
Particular topics of the lecture include: affine and projective complex algebraic curves, intersection multiplicities, Bézout's theorem, Riemann surfaces, the degree-genus formula, the Weierstrass ℘-function, holomorphic differentials, the Riemann-Roch theorem, and curve singularities. Along the way, we will repeatedly encounter elliptic curves and show in multiple ways that their points satisfy a natural group structure. The image on this page is taken from Kirwan's book and illustrates the associativity of this group structure.
Prerequisites
The first two bachelor years.
Program
For our weekly topics and the exercise series, see the course's Moodle page.
Literature
Kirwan's book is the main source for the course:
F. Kirwan: Complex Algebraic Curves
Further reading:
W. Fulton: Algebraic Curves. An introduction to algebraic geometry
E. Brieskorn, H. Knörrer: Ebene algebraische Kurven
E. Ghys: A singular mathematical promenade
