Komplexe Algebraische Kurven

Proseminar Komplexe Algebraische Kurven
Herbstsemester 2019 in Fribourg
Donnerstags von 15h15-17h im Hörsaal 2.52 im Physikgebäude PER 08

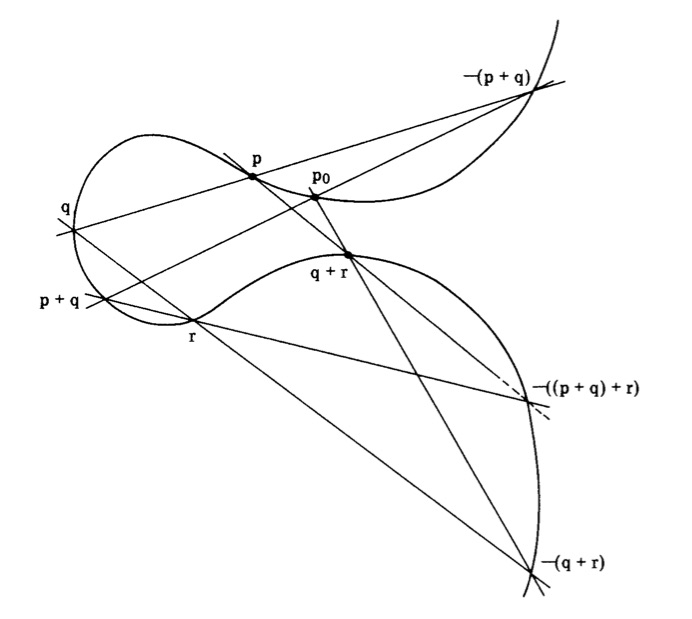
Inhalt. Eine komplexe algebraische Kurve in C^2 ist die Nullstellenmenge eines Polynoms f in C[x,y], wie zum Beispiel f(x,y) = x^3+x^2-y^2+1. Seit Newton steht das Studium der komplexen algebraischen Kurven in fruchtbarer Wechselwirkung mit Ideen aus der Algebra, der Zahlentheorie, der Topologie und der Geometrie, und ist dadurch zu einem zentralen Gegenstand der modernen Mathematik geworden. Die Quelle für das Seminar ist das Buch Complex Algebraic Curves von Frances Kirwan, erschienen in London Mathematical Society Student Texts 23, Cambridge University Press, Cambridge, 1992. Wir werden komplexe algebraische Kurven unter algebraischen, typologischen und komplex-analytischen Gesichtspunkten studieren. Nebenbei werden wir immer wieder kubische Kurven antreffen und auf verschiedene Weise beweisen, dass die Punkte einer kubischen Kurve einer natürlichen Gruppenstruktur gehorchen. Das Bild rechts stammt aus Kirwans Buch und illustriert den Beweis der Assoziativität dieser Gruppenstruktur. (Ein detailliertes Programm der Vorträge befindet sich weiter unten auf dieser Seite).

Organisatorisches.

Das Seminar findet während des Herbstsemesters Donnerstags von 15h15-17h im Hörsaal 2.52 statt. Je nach Zahl der Teilnehmenden kann es einzelne Zusatztermine Donnerstags von 17-19h geben.
Vorkenntnisse für das Seminar sind die Grundlagenvorlesungen aus den ersten zwei Bachelorjahren.
Termine für Vorbesprechungen der Vorträge auf Anfrage. Reservierte Zeiten während des Semesters sind Dienstags 10-13h und Donnerstags 12-15h.
Anmeldung oder Fragen an: livio.liechti(wasstehthierwohl)unifr.ch

Validierungskriterien sind

regelmässige Präsenz im Seminar,
einen zweistündigen Vortrag vorbereiten und an der Wandtafel halten. Die Vorträge können auf Deutsch, Französisch oder Englisch gehalten werden,
ein schriftliches Thema zum Seminar kurz und sauber auf maximal zehn Seiten in LaTeX ausarbeiten. Die hierzu möglichen Themen werden während des Semesters bekanntgegeben.

Detailprogramm.

Datum	15h15-17h	17h15-19h (Reserve)
19. Sept. 2019	Affine ebene Kurven und die projektive Ebene (Seraina Tschan) Abschnitte 2.1 und 2.2 in Kirwan, Seiten 29-40, inklusive Übung 2.7.
26. Sept. 2019	Projektive ebene Kurven (Albin Aliu) Abschnitte 2.3 und 2.4 in Kirwan, Seiten 40-45, inklusive Übungen 2.8 und 2.11, mit eventueller Erwähnung der Fermatschen Vermutung, wie in Abschnitt 1.2.1.
3. Okt. 2019	Die Resultante und eine schwache Version von Bézout (Alison Bender) Abschnitt 3.1 in Kirwan, bis und mit Bemerkung 3.13. inklusive der Beweise von Lemmas 3.3-3.7, Seiten 51-56 und 67-69.
10. Okt. 2019	Schnittzahlen und die starke Version von Bézout (Marina Cotting) Abschnitt 3.1 in Kirwan, Satz 3.18 bis und mit Korollar 3.25, Seiten 59-66.
17. Okt. 2019	Wendepunkte und kubische Kurven (Andrea Tettamanti) Abschnitt 3.2 in Kirwan, Seiten 70-77. Gruppenstruktur auf einer kubischen Kurve (Satz 3.38), ohne Assoziativität.
24. Okt. 2019	Der Hilbertsche Nullstellensatz (Romain Bürgy) "Another Elementary Proof of the Nullstellensatz" von Enrique Arrondo und "Munshi's proof of the Nullstellensatz" von Peter May
31. Okt. 2019	Riemannsche Flächen und holomorphe Abbildungen (Laurence Morard) Abschnitt 5.2 in Kirwan, Definition 5.25 bis und mit Beispiel 5.42, Seiten 125-136.
7. Nov. 2019	Grad-Geschlechtsformel I: Verzweigte Überlagerungen, Triangulierungen und Geschlecht (Hans-Andrea Danuser) Abschnitte 4.2 und 4.3 in Kirwan, Seiten 94-103.
14. Nov. 2019	Grad-Geschlechtsformel II: Beweis (David Bernhard) Abschnitt 4.3 in Kirwan, Seiten 104-109, mit einem eventuellen Abstecher in die Appendizes B und C.
21. Nov. 2019	Die Weierstrasssche p-Funktion (Michaël Vaucher) Abschnitt 5.1 in Kirwan, ab ca. Satz 5.8, Seiten 114-124, und Proposition 5.43 in Abschnitt 5.2, Seiten 137-138.
28. Nov. 2019	Holomorphe Differentiale (Amélie Uldry) Abschnitt 6.1 in Kirwan, Seiten 143-152.
5. Dez. 2019	Der Satz von Abel (Mathias Blaise) Abschnitt 6.2 in Kirwan, Seiten 152-158, und Übung 6.4 auf Seite 178.
12. Dez. 2019	Riemann-Roch I: Der Satz von Riemann (Justine Rosset) Abschnitt 6.3 in Kirwan, Seiten 159-168, bis und mit Beweis von Lemma 6.42, aber ohne Beweis von Riemann-Roch (Satz 6.37).
19. Dez. 2019	Riemann-Roch II: Beweis (Christoph Jutzet) Abschnitt 6.3 in Kirwan, Seiten 168-177, ab Beweis von Proposition 6.31; erst zur Motivation und Erinnerung den Beweis von Riemann-Roch (Satz 6.37).